Event Horizon Miner
L-CLICK TO PLACE A MINING STATION
R-CLICK TO END TURN
PRESS R TO RESTART GAME
-
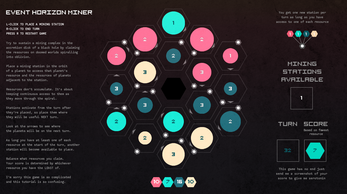
Try to sustain a mining complex in the accretion disk of a black hole by claiming the resources on doomed worlds spiralling into oblivion.
Place a mining station in the orbit of a planet to access that planet's resource and the resources of planets adjacent to the station.
Resources don’t accumulate. It’s about keeping continuous access to them as they move through the spiral.
Stations activate from the turn after they’re placed, so place them where they will be useful NEXT turn.
Look at the arrows to see where the planets will be on the next turn.
As long you have at least one of each resource at the start of the turn, another station will become available to place.
Balance what resources you claim. Your score is determined by whichever resource you have the LEAST of.
I’m sorry this game is so complicated and this tutorial is so confusing.
This game has no end just put a screenshot of your score in the comments to give me serotonin.
| Status | Released |
| Platforms | HTML5 |
| Author | lukenofurther |
| Genre | Simulation, Survival |
| Made with | GameMaker |
| Tags | Abstract, Economy, Futuristic, mind-bending, Short, Singleplayer, Space Sim, Tycoon |
Comments
Log in with itch.io to leave a comment.
nice idea !
It is easy though, to find 1 or 2 moves that you just need to repeat to play endlessly
also use something other than space for end-turn please. Space scrolls the page instead rendering the game unplayable once you access comments.
Thank you - this is really useful feedback! And very timely as this Game Jam isn't finished yet - I've updated the tutorial to reflect the fact you're 'claiming' resources, not accumulating them. I've also made the end turn command R-Click instead of Spacebar.
Wow, thanks! I'd post a screenshot but itch won't let me (I guess the image is too big and my internet times out maybe?) In any case, my best score so far is 40 :)
https://imgur.com/a/kvMm0Y1
I believe the best possible score is 60 but it's a 1/4 to get it instead of 54 even if you wait the eons to get perfect RNG to put the stations down on, since you need the planet that comes in to move one of the scores from 54 to 60. Conveniently, if you achieve this, all of your scores will be exactly 60 ^^
Math:
Let us characterize the score for each color as the sum of the scores obtained on planets of that color. There are 18 planets, 5 of which will be bordered by 16 stations, 5 by 14, 7 by 12, and 1, the top central planet on which we can have no stations, by 6.
The formula 16A_n+14B_n+12C_n+6D_n gives us the score for the nth color, where A_n,B_n,etc correspond to the number of planets with the appropriate number of stations (16 for A, 14 for B, etc) in that color.
Fiddling with a matrix of the relevant equations, we can arrive at:
2 Class-A and 2 Class-B planets for two colors,
1 Class-A and 1 Class-B and 2 Class-C and the 1 Class-D for one color
5 Class-C for the final color
or an equivalent configuration with each color scoring 60. In order for any color to score higher, points would have to be removed from one of the other colors, meaning that the score of the lowest scoring color can't be above 60, so 60 is the maximum high score. However, it requires the planets to be in only a handful of possible positions out of ~69 billion (4^18). Good luck if you decide to go for it, I haven't calculated the actual exact odds yet but I bet the expected number of turns required to achieve it is very high.
Note that you cannot accumulate resources-- you just get a mining station or don't; additional resources are lost at end of turn and don't contribute to score.